Page 4 - Inference of field reversed configuration topology and dynamics during Alfvenic transients

ARTICLE
NATURE COMMUNICATIONS | DOI: 10.1038/s41467-018-03110-5
0.8 0.6 0.4 0.2
0 0.8
0.6 0.4 0.2
0 0.8
0.6 0.4 0.2
0 0.8
0.6 0.4 0.2
0 0.8
0.6 0.4 0.2
0 0.8
0.6 0.4 0.2
0 0.8
0.6 0.4 0.2
30
20
10
0 30
20 10
0 30
20 10
0
30
20
10
0
30
20
10
0 30
20 10
0 30 20 10 0
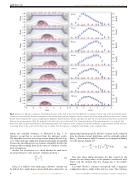
Fig. 3 Inference of Alfvenic oscillations. Poloidal flux structure at the start of the C-2U shot #49040. Left panels: Contour map of the poloidal flux and its evolution in 10 μs intervals. External (red squares) and internal (blue squares) magnetic sensor locations are shown along with the vacuum vessel contour (black) intersecting the flux contours. Right panels: Magnetic field predictions (black) superimposed with the corresponding external (red) and internal (blue) probe measurements (after the magnetic field offset at t = 0 is subtracted). The forward prediction of the measurements is so accurate that differences with actual measurements are barely distinguishable. The frequency of the oscillations around the mid-plane is approximately 20 kHz. The flux- conserving effect of the vessel on this fast scale is evident from the absence of magnetic field change on the external probes
0
–3 –2 –1 0 1 2 3–3 –2 –1 0 1 2 3
z (m) z (m)
within one standard deviation, as illustrated in Fig. 5. So Newton’s second law is recovered from the inference results. The algorithm, however, is not very accurate during the first 50 μs or so of the discharge (right after formation/merging) presumably because the smoothing prior used cannot adequately describe the abrupt profiles resulting from shock waves or violations of other prior assumptions.
Another test of relevance is to check whether the axial forces are proportional to some measure of plasma position z
∂FzffiFz ð3Þ ∂z z
If Eq. (3) is valid for some axial range, a Hooke’s constant can be defined. For a rigid plasma current distribution subjected to an
infinitesimal displacement, the Hooke’s constant can be evaluated from the plasma current distribution and the externally applied flux ψext (from magnets and FC currents) as an integral extending over the plasma domain Ω21
60 μs
70 μs
80 μs
90 μs
100 μs
110 μs
120 μs
∂F ZZ∂2ψ
z 1⁄4 2π jφ ext drdz ð4Þ
Note that when taking derivatives the flux created by the plasma does not change with z, as the plasma is considered a rigid object; only the external flux does change due to the relative motion.
A positive Hooke’s constant corresponds with a magnetic configuration that is axially stable and vice versa. The evolution
kz 1⁄4
∂z ∂z2
4 NATURE COMMUNICATIONS | (2018)9:691
| DOI: 10.1038/s41467-018-03110-5 | www.nature.com/naturecommunications
R (m) R (m) R (m) R (m) R (m) R (m) R (m)
B (mT) B (mT) B (mT) B (mT) B (mT) B (mT) B (mT)